前回は構造物の「静定・不静定」について解説し、見分ける方法として判別式を紹介しました。
今回は判別式について、例題を交えながら詳しく解説していきます!
「静定・不静定」を正しく判別することは構造力学の問題を解くうえで大切なことです。
この記事で「判別式」の使い方を覚えて、今後の学習に活かして下さい!
それではいきましょう~♪
判別式のおさらい
前回、構造物の「静定・不静定」、「安定・不安定」を見分ける方法として、判別式を紹介しました。

構造物の種類を知りたいものに対して、判別式を使って不静定次数 m を求めます!
m > 0 のとき不静定構造物、m = 0 のとき静定構造物、m < 0 のとき不安定構造物と判断することができました。
ここからは、判別式についてもう少し詳しく説明していきます!
反力の数え方
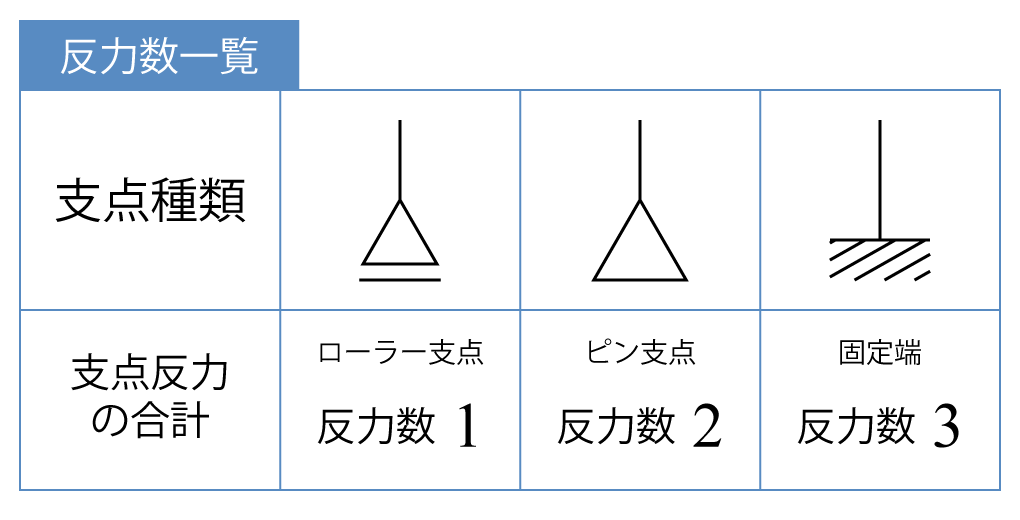
反力の数は支点の種類によって変わります。
各支点における反力の数はこのようになります!
剛節接合部材数の数え方
剛節接合部材数も接合部の形状によって変化します。
各接合部における剛節接合部材数の数え方は次のとおりです!
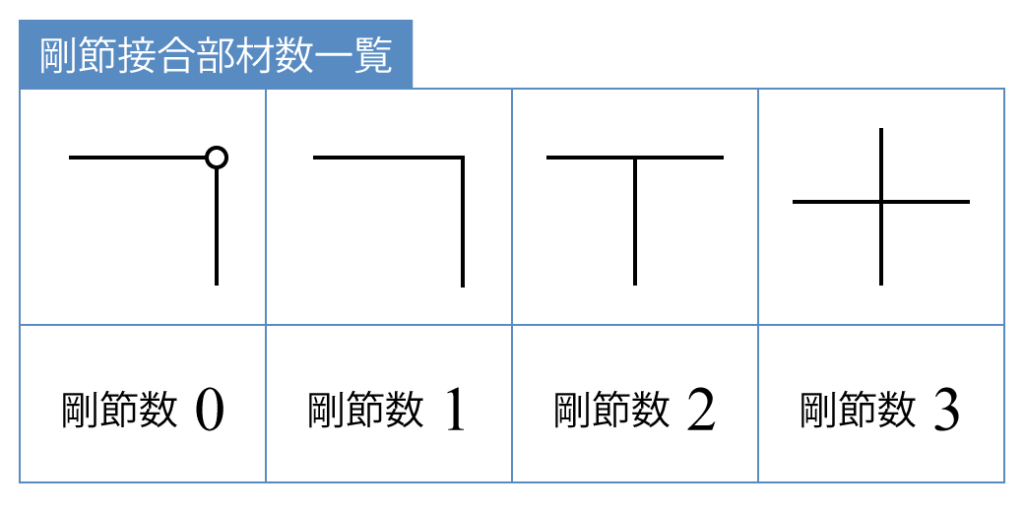
剛接合されている部材の数 ‐1 が剛節接合部材数と覚えて下さい!
問題編
ここからは例題を通して、判別式の使い方をマスターしましょう!
例題①
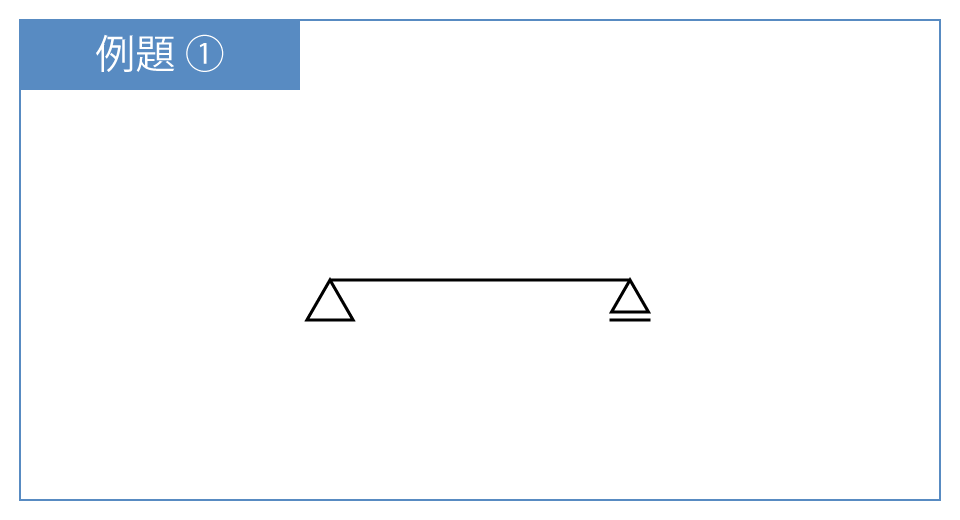
最初は、単純梁の問題です。
まずは自分の手を動かして、解いてみましょう!
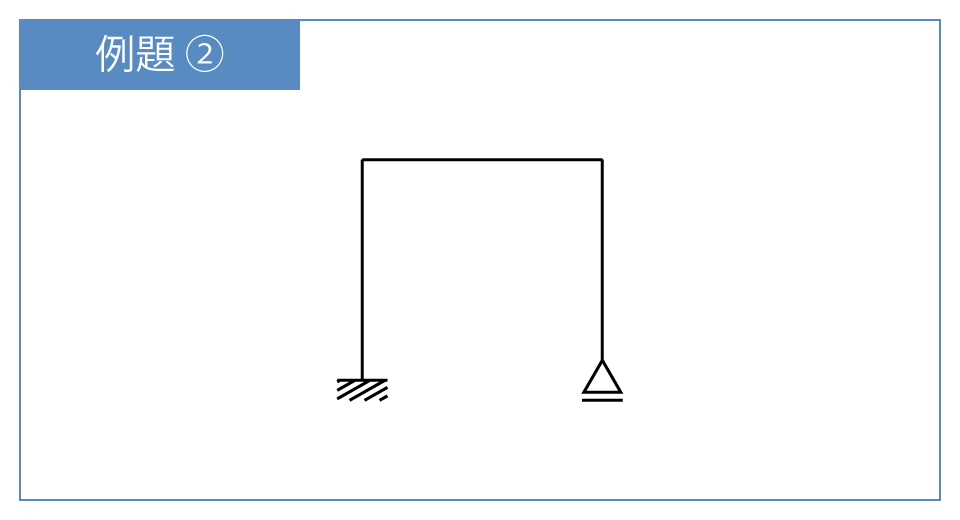
例題②
次は、下のラーメン構造に判別式を使ってみましょう。
すぐに答えは見ずに、まずは自分の力で!
例題③
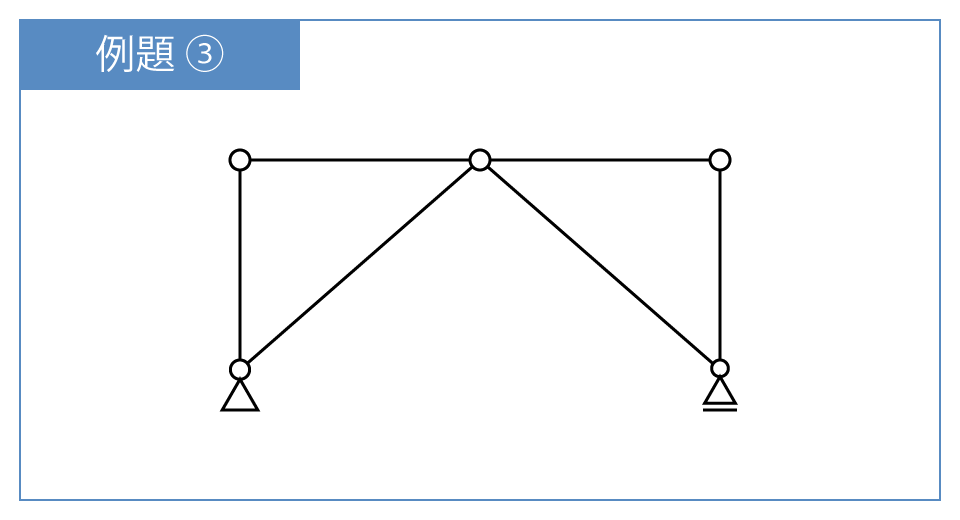
最後はトラス構造の問題です。
ラストスパート、ファイト~♪
解答&解説編
お疲れ様でした!
ここからは解答&解説です。
例題①のこたえ
判別式を使って不静定次数 m を求めるために必要な値を考えます‼
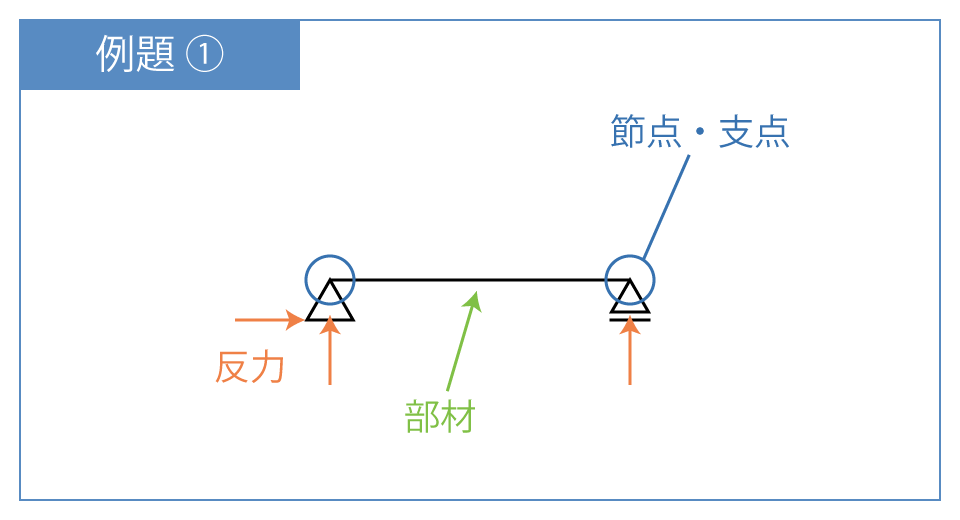
反力数はピン支点(反力数:2)とローラー支点(反力数:1)が1つずつなので反力数は n=3
単純梁なので部材数は s=1
剛接合された部分はないので、剛節接合部材数は r=0
節点・支点数はピン支点とローラー支点の2つなので k=2
よって、不静定次数 m は
m=n+s+r-2k
m=3+1+0-2×2=0
不静定次数 m が 0 なので,この単純梁は静定構造物と判別できました!
例題②のこたえ
例題①と同じように不静定次数 m を求めるために必要な値を考えていきます。

反力数は固定端(反力数:3)とローラー支点(反力数:1)が1つずつなので n=4
部材数は s=3
剛節接合部材数は 2つの材を剛接合した部分が 2つあるので、
剛節接合部材数は r=(2-1)×2=2
節点・支点数は k=4
よって、
m=4+3+2-2×4=1
不静定次数 m が 0 より大きいので,このラーメン構造は不静定構造物となります。
例題③のこたえ
これまでと同じように、不静定次数 m を求めるために必要な値をカクニンします。
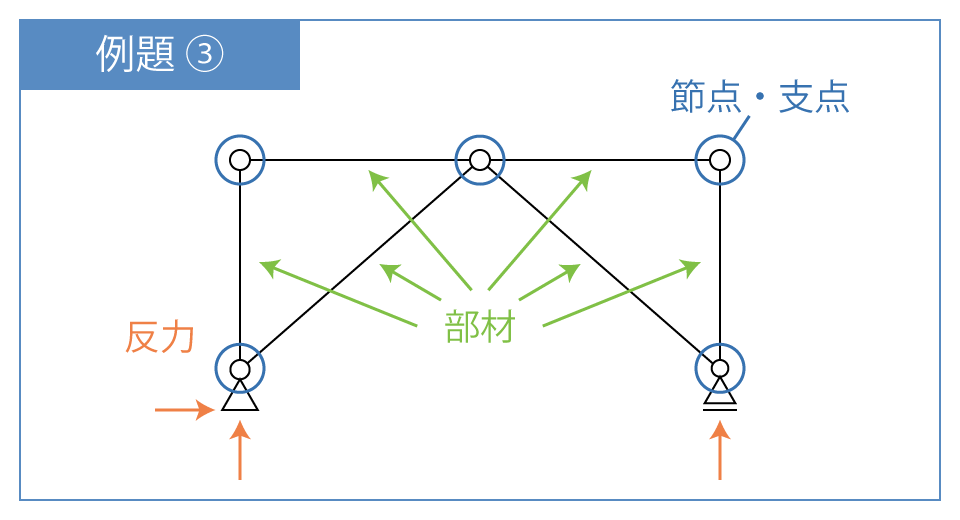
反力数はピン支点とローラー支点が1つずつなので、 n=3
部材数は s=6
すべての部材がピン接合されているので、剛節接合部材数は r=0
節点・支点数は k=5
よって、
m=3+6+0-2×5=-1
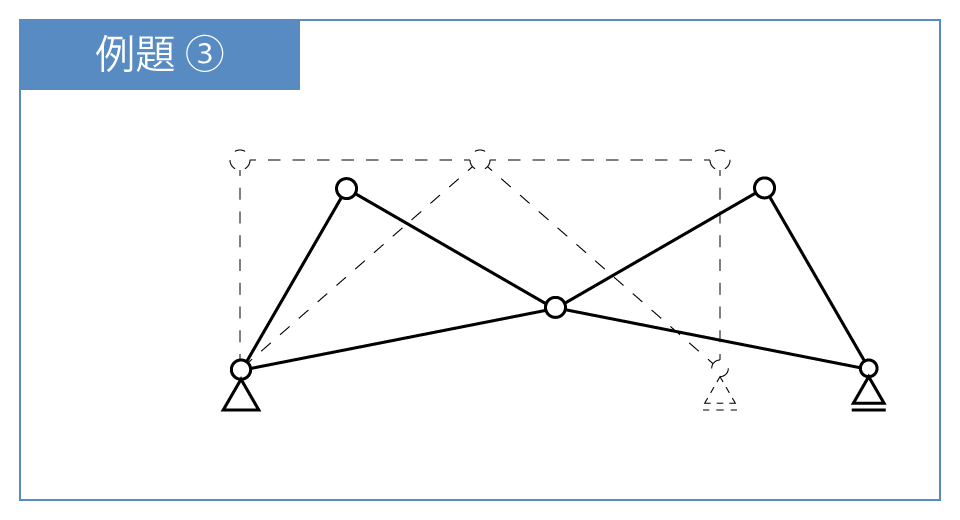
不静定次数 m が 0 より小きいので,このトラス構造は不安定構造物です!
下の図のように崩壊してしまいます…
例題をやってみて、どうでしたか?
「できた‼」という人もいれば、「難しかった…」という人もいるでしょう。
でも大丈夫!これから解けるようになれば大丈夫です‼
まとめ
今回は判別式の使い方を例題を交えて開設しました!
「静定・不静定」、「安定・不安定」を正しく見分けることは、構造力学の問題を解くうえでとても重要です。
そのためにも、判別式の使い方をマスターして今後の学習に活かして下さいね!
とても便利な判別式ですが、結果が違うこともあります。
判別式が使えない場合については、また別の記事で解説します。
最後まで読んでいただき、ありがとうございました。
こんな内容について、書いてほしいといった要望があればぜひコメントお願いします!
ではまた



コメント